Life and death in black and white

A cellular automaton is a is a pattern of cells on a grid, in which the state of each cell changes over multiple time steps based on certain rules.

Life

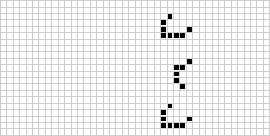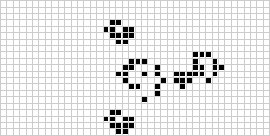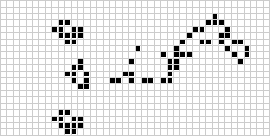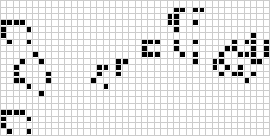
For example, Conway's Game of Life is a cellular automaton which consists of cells on a two-dimensional square grid. The state of each cell is either live or dead, and is updated every time step based on its own state and the states of the 8 cells adjacent to it:

• if a live cell has less than 2 live neighbours, it dies
• if a live cell has exactly 2 or 3 live neighbours, it remains alive
• if a live cell has more than 3 live neighbours, it dies
• if a dead cell has exactly 3 live neighbours, it becomes a live cell

Starting from an initial pattern of cells, the state of the grid in each subsequent time step can be continuously generated to visualise the evolution of the pattern over time:

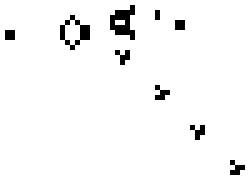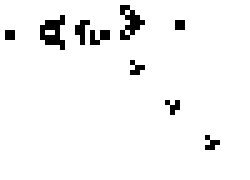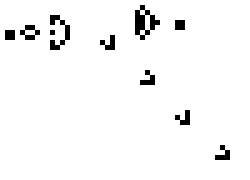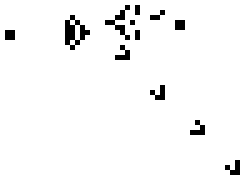
Elementary cellular automata

An elementary cellular automaton (Wikipedia, Wolfram MathWorld) is another specific type of cellular automaton which exists on a one-dimensional grid (a single row of cells) instead. The state of each cell is also either live or dead, or on and off, and updated every time step based its own state and the states of its two neighbours.

Rules

The table above shows how the state of a single cell can be updated in each time step. The first row contains the 8 possible combinations of its own and its two neighbours’ states, and the second row describes what the resulting state for the middle cell should be in the next time step.

This set of state transitions defines an elementary cellular automaton and is known as its rule. The 8 possible configurations of preceding states and two possible resulting states each give a total of 2⁸ or 256 possible combinations of state transitions and hence rules for elementary cellular automata.

The numbering system for rules is known as the Wolfram code and comes from the representation of the state transitions in binary:

If we interpret the 8 resulting states as a binary number, we get 00111100—or 60 in decimal—hence the labelling of this rule as rule 60.

Visualisation

Since a elementary cellular automaton is one-dimensional, a two-dimensional image is enough to visualise its evolution over time. This is done by concatenating multiple rows of cells representing consecutive time steps along a second axis.

This is a visualisation of a 10-cell-wide rule-60 cellular automaton with random initial state:

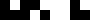
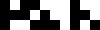
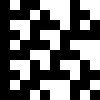
Some larger visualisations:

Edge behaviour

What about the cells at the two ends which only have one neighbour? I'm not sure if there's a standard way to handle this, but there are 4 main options to choose from:

• Treat the cells beside each end as always off (this is the behaviour I used for the visualisations above).
• Treat the cells beside each end as always on.
• Treat the cells beside each end as having the same state as the cell next to them (reflection). For example, if the leftmost cell is on, treat its left neighbour as on as well.
• Treat the cells beside each end as having the same state as the cell on the opposite end (wrapping)—this is like having your simulation take place on a cylinder and the cells on each end are actually touching each other.

(Alternatively, you could also arbitrarily fix or randomise their states if you so wanted.)

Simulating elementary cellular automata

Here's a small function in Python which will generate the next state for a elementary cellular automaton in the form of a string of 1s and 0s:

# lookup table
patterns = ('111', '110', '101', '100', '011', '010', '001', '000')

def next_state(rule, state, edge_behavior='off'):
    # convert the rule number to 8 binary digits, eg. 60 -> 00111100
    table = format(rule, '08b')

    # create an intermediate state with two "virtual" cells at both ends
    if edge_behavior == 'off':
        intermediate = '0' + state + '0'
    elif edge_behavior == 'on':
        intermediate = '1' + state + '1'
    elif edge_behavior == 'mirror':
        intermediate = state[0] + state + state[-1]
    elif edge_behavior == 'wrap':
        intermediate = state[-1] + state + state[0]
    else:
        raise TypeError('invalid value for edge_behavior')

    # lookup the next state for each cell using a sliding window of size 3 over the intermediate state
    # and join everything together
    return ''.join(table[patterns.index(intermediate[i:i + 3])] for i in range(0, len(intermediate) - 2))

Sample usage:

In [2]: r = 60
   ...: s = '1000000000'
   ...: print(s)
   ...: for _ in range(9):
   ...:     s = next_state(r, s)
   ...:     print(s)
   ...:
1000000000
1100000000
1010000000
1111000000
1000100000
1100110000
1010101000
1111111100
1000000010
1100000011

On a proper grid, the output would look like this:

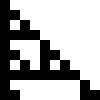
Conclusion

Elementary cellular automata follow simple rules but can develop complex and interesting patterns. Not just cosmetic, elementary cellular automata can model real world systems such as majority voting, traffic flow and allegedly random number generation.

Keep in mind that elementary cellular automata are just a specific type of one-dimensional cellular automata. You've possibly interacted with cellular automata in many other places before: falling sand games, fluid simulation such as in Minecraft, Terraria and Dwarf Fortress, creature simulation, cave generation and more, all can be done with cellular automata.